Codage de l'information

Alors que les hommes comptent avec dix chiffres, de 0 à 9, les ordinateurs n'utilisent que deux chiffres, 0 et 1. Dans le premier cas il s'agit de la numération décimale, ou en base 10, et dans le second cas c'est la numération binaire, ou en base 2.
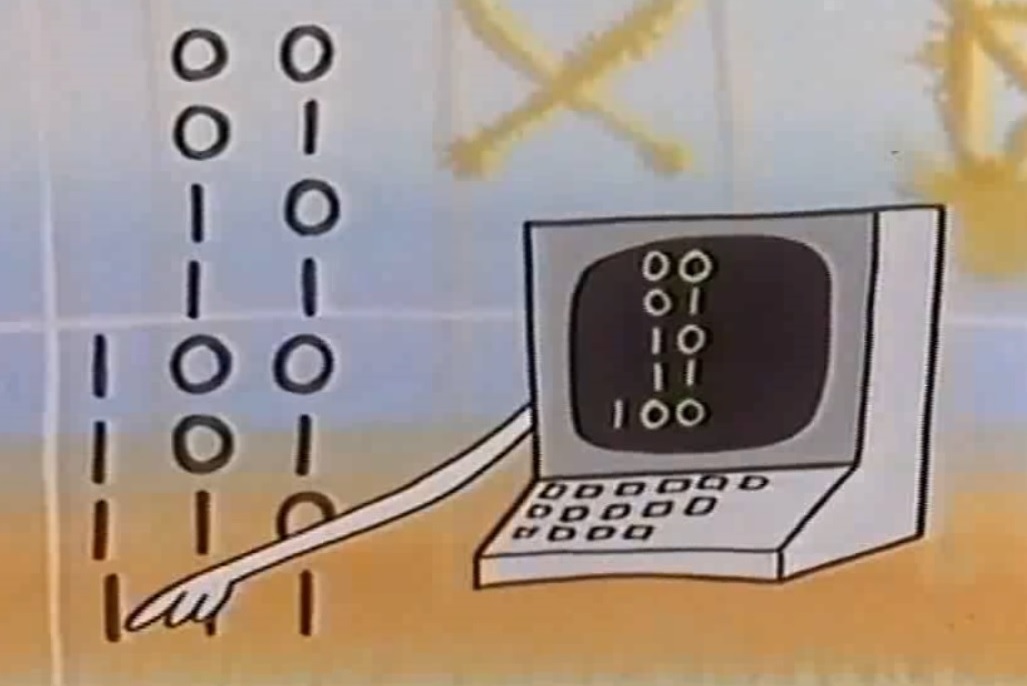
Si on utilise un nombre à trois chiffres binaires pour compter, cela donne:
| binaire | décimal | ||
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 2 |
| 0 | 1 | 1 | 3 |
| 1 | 0 | 0 | 4 |
| 1 | 0 | 1 | 5 |
| 1 | 1 | 0 | 6 |
| 1 | 1 | 1 | 7 |
On remarque que:
- 0012 (le 2 en indice signifie que le nombre est en base 2) vaut 110 (le 10 en indice signifie que le nombre est en base 10),
- 0102 vaut 210,
- 1002 vaut 410.
On peut continuer indéfiniment, les chiffres binaires qui composent le nombre correspondent, en décimal, à des puissances de 2. On en déduit une formule mathématique pour décoder un nombre en base 2, c'est à dire le convertir en décimal:
dn ... d1 d02 = (d0 × 20 + d1 × 21 + ... + dn × 2n)10
Exemples:
- 1102 = (0 × 20 + 1 × 21 + 1 × 22)10 = (0 × 1 + 1 × 2 + 1 × 4)10 = (0 + 2 + 4)10 = 610
- 101 10112 = (1 × 20 + 1 × 21 + 0 × 22 + 1 × 23 + 1 × 24 + 0 × 25 + 1 × 26)10 = (1 × 1 + 1 × 2 + 0 × 4 + 1 × 8 + 1 × 16 + 0 × 32 + 1 × 64)10 = (1 + 2 + 0 + 8 + 16 + 0 + 64)10 = 9110
Définitions:
- Un chiffre binaire s'appelle un bit. Ce nom provient des mots anglais "BInary digiT", qui signifient "chiffre binaire".
- Dans un nombre en binaire, le chiffre à l'extrême droite s'appelle le LSB. Cela provient de l'abréviation des mots anglais "Least Significant Bit", qui se traduit par "bit de poids faible".
- Dans un nombre en binaire, le chiffre à l'extrême gauche s'appelle le MSB. Cela provient de l'abréviation des mots anglais "Most Significant Bit", qui se traduit par "bit de poids fort".

Exercices de décodage du binaire:
Complétez le tableau ci-dessous en comptant, à partir de 010, avec un nombre à 5 chiffres et en base 2:
| binaire | décimal | ||||
Ajoutez, si besoin, un commentaire:
Décodez les nombres en base 2 suivants:
- 1011 01112 =
( × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 )10 =
( × + × + × + × + × + × + × + × )10 =
( + + + + + + + )10 =
10Ajoutez, si besoin, un commentaire:
- 10 0110 01102 =
( × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 )10 =
( × + × + × + × + × + × + × + × + × + × )10 =
( + + + + + + + + + )10 =
10Ajoutez, si besoin, un commentaire:
- 11 1001 10012 =
( × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 + × 2 )10 =
( × + × + × + × + × + × + × + × + × + × )10 =
( + + + + + + + + + )10 =
10Ajoutez, si besoin, un commentaire:
Codage en binaire
Il existe deux méthodes pour coder du décimal en binaire:
- En utilisant la division Euclidienne. Cela donne une méthode facile à programmer, parce qu'elle découle d'un raisonnement mathématique.
- En faisant un tableau pour décomposer le nombre décimal sur des puissances de 2. C'est la méthode la plus simple à utiliser.
Méthode de la division Euclidienne:
On réalise des divisions successives par 2, le reste de chaque division est le chiffre binaire d'ordre précédent. Ainsi, pour la nième division par 2, le reste est le chiffre binaire d'ordre n - 1.
Exemple:
Codage binaire de 6710:| 67 | 2 | |||||
| 1 | 33 | 2 | ||||
| 1 | 16 | 2 | ||||
| 0 | 8 | 2 | ||||
| 0 | 4 | 2 | ||||
| 0 | 2 | 2 | ||||
| 0 | 1 |
Donc 6710 = 100 00112.
Méthode de la décomposition sur des puissances de 2:
On va coder 18310 en binaire pour illustrer la méthode:
- On commence par chercher la puissance de 2 qui est inférieur au nombre à coder et qui s'en approche le plus:
- 20 = 1,
- 21 = 2,
- 22 = 4,
- 23 = 8,
- 24 = 16,
- 25 = 32,
- 26 = 64,
- 27 = 128,
- 28 = 256.
Ensuite on fait un tableau avec, de droite à gauche, la plus petite puissance de 2 jusqu'à celle trouvée à l'étape précédente:
27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 Codage en binaire: Reste: Pour remplir le tableau, on procède comme suit:
- Comme 128 est inférieur à 183, on met 1 dans la case en dessous de 27. Il reste 183 - 128 = 55.
- Comme 64 est supérieur à 55, on met 0 dans la case en dessous de 26. Il reste toujours 55.
- Comme 32 est inférieur à 55, on met 1 dans la case en dessous de 25. Il reste 55 - 32 = 23.
- Comme 16 est inférieur à 23, on met 1 dans la case en dessous de 24. Il reste 23 - 16 = 7.
- Comme 8 est supérieur à 7, on met 0 dans la case en dessous de 23. Il reste toujours 7.
- Comme 4 est inférieur à 7, on met 1 dans la case en dessous de 22. Il reste 7 - 4 = 3.
- Comme 2 est inférieur à 3, on met 1 dans la case en dessous de 21. Il reste 3 - 2 = 1.
- Comme le dernier reste est 1, il faut mettre 1 dans la case en dessous de 20. Il reste 0 et la conversion est terminée.
Le tableau complété est:
27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 Codage en binaire: 1 0 1 1 0 1 1 1 Reste: 55 55 23 7 7 3 1 Donc 18310 = 1011 01112.

Exercices de codage en binaire:
Coder en binaire, avec la méthode de la division Euclidienne, les nombres décimaux ci-dessous:
-
Codage en binaire de 8710:
87 2 2 2 2 2 2 Donc 8710 = 2.
Ajoutez, si besoin, un commentaire:
-
Codage en binaire de 23110:
231 2 2 2 2 2 2 2 Donc 23110 = 2.
Ajoutez, si besoin, un commentaire:
-
Codage en binaire de 74510:
745 2 2 2 2 2 2 2 2 2 Donc 74510 = 2.
Ajoutez, si besoin, un commentaire:
Coder en binaire, avec la méthode de la décomposition sur des puissances de 2, les nombres décimaux ci-dessous:
-
Codage en binaire de 17310:
27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 Codage en binaire: Reste: Donc 17310 = 2.
Ajoutez, si besoin, un commentaire:
-
Codage en binaire de 47010:
28 = 256 Codage en binaire: Reste:
27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 Codage en binaire: Reste: Donc 47010 = 2.
Ajoutez, si besoin, un commentaire:
-
Codage en binaire de 94110:
29 = 512 28 = 256 Codage en binaire: Reste:
27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 Codage en binaire: Reste: Donc 94110 = 2.
Ajoutez, si besoin, un commentaire:
Jeux en ligne
Vous pouvez tester vos connaissances avec les jeux en ligne suivants:
(cc) j. ahmad - Education Nationale - 2020